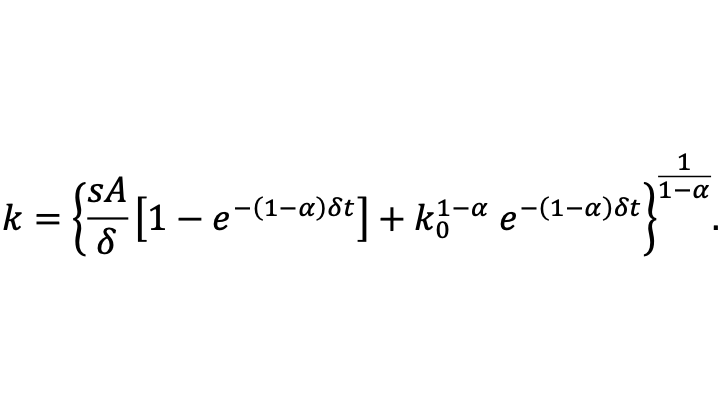The formula for capital per worker k is therefore a constant-elasticity-of-substitution (CES) aggregate between the initial level of capital per worker and the steady-state level of capital per worker k* given above, with elasticity of substitution equal to 1/α > 1 and a weight on the initial level of capital per worker that starts at 1 and exponentially decays at the rate (1-α)δ with the steady-state level of capital per worker k* having a complementary weight such that the two weights add to 1.
The formula for capital per worker, which drives all the other evolving variables in the model, implies that the convergence rate is equal to (1-α)δ. (That convergence rate generalize to cases with other production functions, as long as α is interpreted as capital’s share at the steady-state level of capital per worker.) This is a quite slow rate of convergence. For example, even if δ is relatively high, at a continuous-time rate of 10.5% per year, convergence would be a continuous-time rate of 7% per year if capital’s share is equal to 1/3. That means by the rule of 70 that the half-life of departures from the steady-state would be ten years, as the economy nears the steady state. (The rule of 70 is simply a consequence of the the natural logarithm of 2 equaling approximately .7.)
At the steady state, capital per worker is unchanging over time. That also means that unchanging at the steady state. Intuitively, investment is enough to compensate for depreciation. If there is population growth, or growth in the effective number of workers beyond population growth because of technological progress, the differential equation and its solution above continue to hold as long as k is interpreted as capital per effective worker and δ is interpreted as
δ = depreciation rate + population growth rate + rate of labor augmenting technological progress.
The power